Background

Numerical Integration: A brief crash couse

Many physical systems can be expressed as a series of differential equations. Euler’s method is the simplest numerical procedure for solving these equations given some initial conditions. In the case of our problem statement:

• We have some initial conditions (such as position and velocity of a planet) and we want to know what kind of orbit this planet will trace out, given that only the force acting on it is gravity.
• Using the physical insight that the “slope” of position over time is velocity, and the “slope” of velocity over time is acceleration, we can predict, or integrate, how the quantities will change over time.
• More explicitly, we can use the acceleration supplied by gravity to predict the velocity of our planet, and then use this velocity to predict its position a timestep \(\Delta t\) later.
• This gives us a new position and the whole process starts over again at the next timestep. Here is a schematic of the Euler integration method.

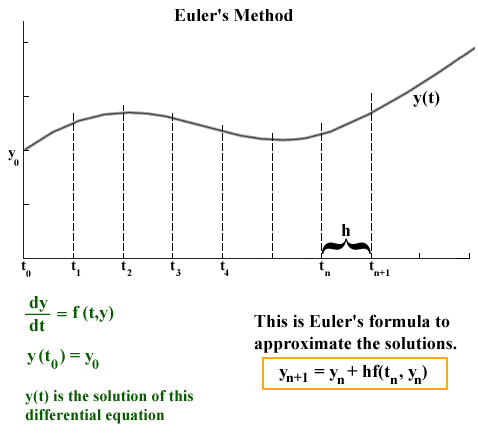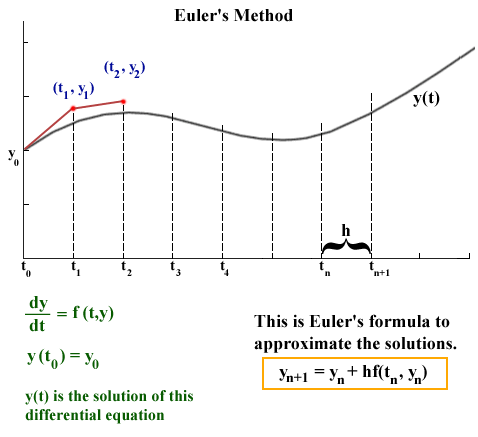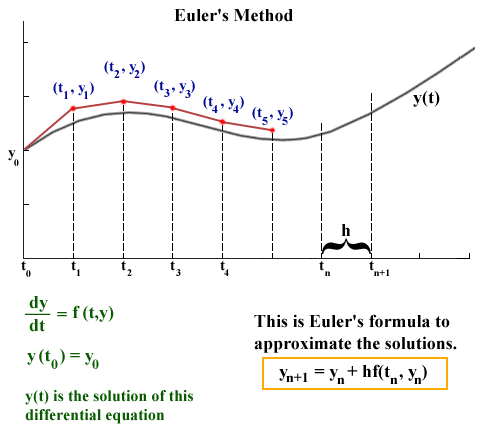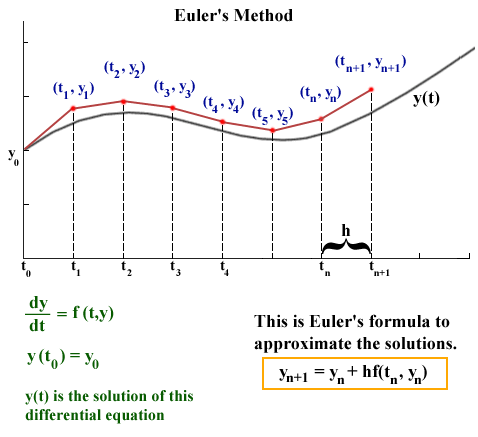
This plot above could represent the component of the planet’s velocity varies over time. Specifically, we have some solution curve (black) that we want to approximate (red), given that we only know two things:

• where we started \((t_0, y_0)\)
• the rate of how where we were changes with time \(\left(\dot{y}_0 \equiv \frac{\mathrm d y_0}{\mathrm{d} t} = \frac{y_1 - y_0}{h}\right)\)

The cool thing about this is that even though we do not explicity know what \(y_1\) is, the fact that we are given \(\dot{y}_0\) from the initial conditions allows us to bootstrap our way around this. Starting with the definition of slope, we can use the timestep \(h \equiv \Delta t = t_{n+1} - t_n\), to find where we will be a timestep later \(\dot{y}_1\):

\[\dot y_0 = \frac{y_1 - y_0}{h}\quad\longrightarrow\quad y_1 = y_0 + h \dot{y}_0\quad.\]

Generalizing to any timestep \(n\):

\[y_{n+1} = y_n + h \dot{y}_n \quad.\]

Whenever all of the \(n+1\) terms are on one side of the equation and the \(n\) terms are on the other, we have an explicit numerical method. This can also be extended to \(k\) components for \(y_n\) with the simple substitution:

\[\begin{split}\newcommand{b}[1]{\mathbf{#1}} y_n \longrightarrow \b X_n = \begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_k\end{pmatrix},\quad \dot{y}_n \longrightarrow \b {\dot X}_n = \begin{pmatrix}\dot{x}_1 \\ \dot{x}_2 \\ \vdots \\ \dot{x}_k\end{pmatrix},\quad y_{n+1} \longrightarrow \b X_{n+1} = \b X_{n} + h \dot{\b X}_n \quad.\end{split}\]

This is intuitively straightforward and easy to implement, but there is a downside: the solutions do not converge for any given timestep. If the steps are too large, our numerical estimations are essentially dominated by progation of error and would return results that are non-physical, and if they are too small the simulation would take too long to run.

We need a scheme that remains stable and accurate for a wide range of timesteps, which is what implicit differentiation can accomplish. An example of one such scheme is:

\[\b X_{n+1} = \b X_{n} + h \dot{\b X}_{n+1} \quad.\]

Now we have \(n+1\) terms on both sides, making this an implicit scheme. This is know as the backward Euler method and a common way of solving this and many other similar schemes that build of off this one is by re-casting it as a root finding problem. For the backward Euler method, this would look like:

\[\b g(\b X_{n+1}) = \b X_{n+1} - \b X_n - h \dot{\b X}_{n+1}\quad.\]

Here, the root of the new function \(\b g\) is the solution to our original implicit integration equation. The Newton-Raphson method is a useful root finding algorithm, but one of its steps requires the computation of the \(k \times k\) Jacobian:

\[ \begin{align}\begin{aligned}\newcommand{\pd}[2]{\frac{\partial#1}{\partial#2}}\\\begin{split}\b{J}(\b {\dot X}_{n+1}) = \pd{\b {\dot X}_{n+1}}{\b X_{n+1}} = \begin{pmatrix} \nabla (\dot x_1)_{n+1} \\ \nabla (\dot x_2)_{n+1} \\ \vdots \\ \nabla (\dot x_k)_{n+1} \\ \end{pmatrix} \quad.\end{split}\end{aligned}\end{align} \]

Note

We avoid using superscript notation here because that will be reserved for identifying iterates in Newton’s method, which we discuss in Example Applications.

spacejam can also support systems with a different number of equations than variables, i.e. non-square Jacobians. See Demo III: Vector function with vector input.

Accurately computing the elements of the Jacobian can be numerically expensive, so a method to quickly and accurately compute derivatives would be extremely useful. spacejam provides this capability by computing the Jacobian quickly and accurately via automatic differentiation, which can be used to solve a wide class of problems that depend on implicit differentiation for numerically stable solutions.

We walk through using spacejam to implement Newton’s method for the Backward Euler method and its slightly more sophisticated siblings, the \(s=1\) and \(s=2\) Adams-Moulton methods in Example Applications. Note: \(s=0\) is just the original backward Euler method and \(s=1\) is also know as the famous trapezoid rule. To the best of our knowledge, there is not a cool name for the \(s=2\) method.

Automatic Differentiation: A brief overview

This is a method to simultaneously compute a function and its derivative to machine precision. This can be done by introducing the dual number \(\epsilon^2=0\), where \(\epsilon\ne0\). If we transform some arbitrary function \(f(x)\) to \(f(x+\epsilon)\) and expand it, we have:

\[f(x+\epsilon) = f(x) + \epsilon f'(x) + O(\epsilon^2)\quad.\]

By the definition of \(\epsilon\), all second order and higher terms in \(\epsilon\) vanish and we are left with \(f(x+\epsilon) = f(x) + \epsilon f'(x)\), where the dual part, \(f'(x)\), of this transformed function is the derivative of our original function \(f(x)\). If we adhere to the new system of math introduced by dual numbers, we are able to compute derivatives of functions exactly.

For example, multiplying two dual numbers \(z_1 = a_r + \epsilon a_d\) and \(z_2 = b_r + \epsilon b_d\) would behave like:

\[\begin{split}z_1 \times z_2 &= (a_r + \epsilon a_d) \times (b_r + \epsilon b_d) = a_rb_r + \epsilon(a_rb_d + a_db_r) + \epsilon^2 a_db_d \\ &= \boxed{a_rb_r + \epsilon(a_rb_d + a_db_r)}\quad.\end{split}\]

A function like \(f(x) = x^2\) could then be automatically differentiated to give:

\[f(x) \longrightarrow f(x+\epsilon) = (x + \epsilon) \times (x + \epsilon) = x^2 + \epsilon (x\cdot 1 + 1\cdot x) = x^2 + \epsilon\ 2x \quad,\]

where \(f(x) + \epsilon f'(x)\) is returned as expected. Operations like this can be redefined via operator overloading, which we implement in Implementation Details. This method is also easily extended to multivariable functions with the introduction of “dual number basis vectors” \(\b p_i = i + \epsilon_i 1\), where \(i\) takes on any of the components of \(\b X_{n}\). For example, the multivariable function \(f(x, y) = xy\) would transform like:

\[\begin{split}\require{cancel} x \quad\longrightarrow\quad& \b p_x = x + \epsilon_x + \epsilon_y\ 0 \\ y \quad\longrightarrow\quad& \b p_y = y + \epsilon_x\ 0 + \epsilon_y \\ f(x, y) \quad\longrightarrow\quad& f(\b p) = (x + \epsilon_x + \epsilon_y\ 0) \times (y + \epsilon_x\ 0 + \epsilon_y) \\ &= xy + \epsilon_y x + \epsilon_x y + \cancel{\epsilon_x\epsilon_y} \\ &= xy + \epsilon_x y + \epsilon_y x \quad,\end{split}\]

where we now have:

\[\begin{split}f(x+\epsilon_x, y+\epsilon_y) &= f(x, y) + \epsilon_x\pd{f}{x} + \epsilon_y\pd{f}{y} = f(x, y) + \epsilon \left[\pd{f}{x},\ \pd{f}{y}\right] \\ &= f(x, y) + \epsilon \nabla f(x, y)\quad.\end{split}\]

This is accomplished internally in spacejam.autodiff.Autodiff._ad with:

    def _ad(self, func, p, kwargs=None):
        """ Internally computes `func(p)` and its derivative(s).
        
        Notes
        -----
        `_ad` returns a nested 1D `numpy.ndarray` to be formatted internally
        accordingly in :any:`spacejam.autodiff.AutoDiff.__init__`  .

        Parameters
        ----------
        func : numpy.ndarray
            function(s) specified by user.
        p : numpy.ndarray
            point(s) specified by user.
        """
        if len(p) == 1: # scalar p
            p_mult = np.array([dual.Dual(p)]) 

        else:# vector p
            p_mult = [dual.Dual(pi, idx=i, x=p) for i, pi in enumerate(p)]
            p_mult = np.array(p_mult) # convert list to numpy array

        # perform AD with specified function(s)
        if kwargs:
            result = func(*p_mult, **kwargs) 
        else:
            result = func(*p_mult) 
        return result

The x argument in the spacejam.dual.Dual class above sets the length of the \(\ p\) dual basis vector and the idx argument sets the proper index to 1 (with the rest being zero).